1660年明永历十四年,清顺治十七年,罕见拉丁文版《亚历山大的帕普斯 数学汇编》
首次印刷于 1588 年,意大利人文主义者和数学家 科曼迪诺(Federico Commandino,1509-1575 年)翻译编辑
1660年是一个闰年,是农历庚子年,是鼠年。年号:大明永历十四年、大清顺治十七年;越南后黎朝永寿三年,莫朝顺德二十三年;日本万治三年。
- 2月,保王党分子、英国驻苏格兰军队司令蒙克率军进驻伦敦。
- 2月29日,清廷以翻译之《三国志》(满文本)颁赐诸王以下、甲喇章京以上官,以使臣僚继承太宗黄台吉的遗愿,讲求治国平天下之道。
- 3月19日,清廷制定了八旗汉字官名:固山额真汉字称为都统,梅勒章京汉字称副都统,甲喇章京汉字称参领,牛录章京汉字称佐领,昂邦章京汉字称总管。
- 3月28日,礼部遵旨拟定王、贝勒、贝子、公等妻女封号:亲王、世子、郡王正室曰妃,贝勒、贝子、镇国公、镇国将军、辅国将军正室曰夫人,奉国将军正室曰淑人,奉恩将军正室曰恭人。亲王女和硕格格曰郡主,世子、郡王女多罗格格曰县主,贝勒女多罗格格曰郡君,贝子女固山格格曰县君,入八分镇国公、辅国公女曰乡君,未入八分镇国公、辅国公及镇国将军以下之女不授封,曰宗女。
- 4月,刚刚复辟上台的查理二世将海上力量定名为“皇家海军”,而拒绝颁发陆军使用“皇家”字样的特许状。
- 4月4日,英王查理二世发表《布雷达宣言》。这是英国历史上斯图亚特王朝复辟时期的开始。
- 4月17日,清廷制定了迟报灾情处分条例。规定:凡各直省有灾,先以情形入告,夏灾限六月、秋灾限七月上报。州县官如逾半月以内者罚俸六个月,一个月以内者罚俸一年,一个月以外者降一级,两个月以外者降二级,三个月以外者革职。抚按道府官以州县报到之日为始,若有逾限,照例一体处分。
- 5月29日,镇守宁古塔总管巴海疏报,侦知罗刹在费雅喀部落西界,乃领兵至使犬地方,在古法坛村(在今俄罗斯伯力附近)一带设伏,斩罗刹60余级,淹死者甚多,获妇女47口,并火炮盔甲器械诸物,抚慰费雅喀部落15村,120余户。
- 5月29日,查理二世在英国复辟。
- 5月——波兰立陶宛联邦放弃波罗的海沿岸利沃尼亚的大部分属地,瑞典在波罗的海势力达到鼎盛时期。
- 6月9日——法国国王路易十四和西班牙公主玛丽·泰蕾莎结婚,使路易成为欧洲权力最大的国王。
- 8月19日,年仅二十二岁的皇贵妃董鄂氏去世。董鄂氏在顺治十三年十二月初六入宫后甚到顺治帝宠爱被封为皇贵妃。
- 9月,波兰—鞑靼联军在楚德诺夫围攻俄军。
- 11月29日,鉴于费雅喀部落头目柴邦阿奴、使犬部落头目哈禅、祁勒尔落头目痕忒克等,进贡黑狐、貂皮,清廷各赏蟒朝衣一袭。
- 11月——英国皇家学会设立,成为近代科学革命的基础
- 5月28日——乔治一世,汉诺威选帝侯、英国国王。(1727年逝世)
- 10月21日,德国医生和化学家施塔尔生于德国的安斯巴赫,早年在耶拿学医。
- 12月4日,法国作曲家康普拉在普罗旺斯地区艾克斯受洗,1744年6月29日卒于凡尔赛。
1660年大明永历十四年,大清顺治十七年,罕见拉丁文版《亚历山大的帕普斯 数学汇编》首次印刷于 1588 年,意大利人文主义者和数学家科曼迪诺(Federico Commandino,1509-1575 年)翻译编辑,平装本,大理石纹纸。奥地利利奥波德·威廉·哈布斯堡大公的骑马肖像,由J.特洛伊恩在特尼尔斯之后雕刻)拉丁文版《亚历山大的帕普斯数学汇编》。
帕普斯:
(Pappus)古希腊数学家。3-4世纪人。也译巴普士。他是亚历山大学派的最后一位伟大的几何学家。生前有大量著作,但只有《数学汇编》保存下来。《数学汇编》对数学史具有重大的意义,这部著作对前辈学者的著作作了系统整理,并发展了前辈的某些思想,保存了很多古代珍贵的数学作品的资料。
帕波斯是亚历山大晚期的数学家。确定他的生活年代,主要的依据是他在注释托勒密的书时提到他最近曾目睹一次日食。经考证,这次日食应发生在公元320年10月18日另外,赛翁(Theon of Alexandria,公元390年前后)编写的一份年代表,手稿现藏在莱顿,旁边有注释者的字迹,对着戴克里先(Diocletian,罗马皇帝,公元284—305年在位)的名字写道:“此时帕波斯写作”,这和前面的日食年代出入不大,可能在戴克里先时代他还年青,刚开始写作。
帕波斯有不少著作,唯一流传下来的正是最有价值的一种:《数学汇编》(Mathematical collection),简称《汇编》(Collection,或Synagoge),synagoge的希腊原文是συναγωγ,是收集,汇集的意思.《汇编》在历史上占有特殊的地位,这不仅仅是它本身有许多发明创造,更重要的是记述了大量前人的工作,保存了一大批现在在别处无法看到的著作.它和普罗克洛斯的《概要》是研究希腊数学史的两大原始资料。
《汇编》原有8卷,卷Ⅰ和卷Ⅱ的前一部分已失传.各卷写于不同的年代,完成全书应在公元320年或340年之后。
目前唯一完善的版本是F.胡尔奇(Hultsch)校订并翻译的希腊文与拉丁文对照本,包括非常宝贵的导言、注解和附录。唯一全部译成现代语的有P.V.埃克(Eecke)的法文译本。选择其中一部分译出的则较多,而最早的拉丁文译本是F.科曼迪诺(Commandino,1509—1575)作出的(1566),只是一部分,以后在17,18世纪及近代又有多种摘要译本。
《数学汇编》共有8篇:第1篇为算术;第2篇提出了连乘法;第3篇关于平面几何与立体几何,其中有寻找两条以知线段的比例中项问题,有关于算术平均、几何平均和调和平均以及把三者表示在一个几何图形上的问题,并揭示了如何把正五面体内接于一个球内;第4篇有关于3个以知圆彼此外切问题,还详细讨论了阿基米德螺线、尼科梅德蚌线及希波克拉提斯割圆曲线问题等,并涉及任何角的三等分问题;第5篇是关于面积和体积问题;第6篇是对先前的天文学家和数学家的著作的评注;第7篇阐述了术语分析和综合以及定理和问题之间的区别;第8篇主要是关于力学。
可惜,《数学汇编》中的一些篇章也已经散佚。此外,巴普士还有注释托勒玫、欧几里得等人著作的其他著述。
公元4世纪,希腊数学已成强弩之末。『黄金时代』﹝300 B.C─200 B.C﹞几何巨匠已逝去五、六百年,公元前146年亚历山大被罗马人占领,学者们虽然仍能继续研究,然而已没有他们的先辈那种气势雄伟、一往无前的创作精神。公元后,兴趣转向天文的应用,除门纳劳斯﹝Menelaus of Alexandria公元100前后﹞、托勒密﹝Claudius Ptolemy,约公元85-165﹞在三角学方面有所建树外,理论几何的活力逐渐凋萎。此时亚历山大的帕普斯(Pappus of Alexandria)正努力总结数百年来前人披荆斩棘所取得的成果,以免年久失传。
帕普斯给欧几里得《几何原本》和《数据》以及托勒密的《大汇编》和《球极平面投影》作过注释。写成八卷的《数学汇编》﹝Synagoge或”Mathematical Collection”﹞──对他那个时代存在的几何著作的综述评论和指南,其中包括帕普斯自己的创作。但第一卷和第二卷的一部份已遗失,许多古代的学术成果,由于有了这部书的存录,才能让后世人得知。例如芝诺多努斯的《等周论》,经过帕普斯的加工,被编入于第五卷之中。当中有关于“圆面积大于任何同周长正多边形的面积”、“球的体积大于表面积相同的圆锥、圆柱”、“表面积相同的正多面体,面积愈多体积愈大”等命题。对于希腊几何三大问题也作了历史的回顾,并给出几种用二次或高次曲线的解法。在第七卷中则探讨了三种圆锥曲线的焦点和准线的性质,还讨论了“平面图形绕一轴旋转所产生立体的体积”,后来这叫做“古尔丁定理”,因为后者曾重新加以研究。
帕普斯,他的主要成就是总结数百年的学者成果,以免年久失传。《数学汇编》引用和参考了三十多位古代数学家的著作,传播了大批原始命题及其进展、扩展和历史注释。由于许多原著已经散失,《数学汇编》便成为了解这些著作的唯一源泉,是名副其实的几何宝库。
阿拉伯人和中世纪的欧洲人几乎不知道帕普斯的《数学汇编》,但在被费德里科·达米诺Federico Commandino翻译成拉丁语后,对17世纪的数学产生了巨大的影响。丢番图的《算术》和帕普斯的《收藏》是维埃特的《分析艺术》(1591年)中《伊萨戈格》的两个主要来源。帕普斯问题及其推广引导笛卡尔发展了解析几何。费马还从帕普斯对阿波罗尼乌斯失落的作品《平面位点》和《论确定部分》的总结中发展了他的解析几何版本以及他的马克西玛和米尼玛的方法。其他受帕普斯影响的数学家有帕乔利、达芬奇、开普勒、范鲁门、帕斯卡、牛顿、伯努利、欧拉、高斯、热贡、施泰纳和庞塞莱特。
科曼迪诺:
科曼迪诺( Commandino, Federico, 1509-1575)意大利数学家.生于乌尔比诺(Urbino ),卒于乌尔比诺.早年在法诺(Fano)学习拉丁语和希腊文,后回家乡学习数学.1534年人帕多瓦(Padua)大学攻读了10年哲学和医学,在费拉拉(Ferrara)大学获医学学位.

科曼迪诺以编辑、翻译和注释古希腊经典数学著作而出名,其中有阿基米德(Archimedes)的《圆的度量》等5部著作(1544)、托勒密(Ptolemy)的《星座图》(1558)、阿波罗尼奥斯(Apollonius, (P))的《圆锥曲线论》(1566)等,以及阿里斯托赛诺斯CArietoxenue )、海伦(Heron, CA. ))、帕普斯(Pap-pus, (A”等人的著作.此外,他还出版了欧几里得(Euclid)的《图形分割》的拉丁文本(1570),并指导学生将《几何原本》译为意大利文(1572).这些工作对传播古希腊科学文化很有帮助.












据说大科学家牛顿曾经出过一个智力趣味题:
九棵果树,排成十行,
每行三棵,问如何栽?
这个题目如果10变成9就是一个经典的定理——帕普斯定理的应用,至于“九树十行”,仅是这个定理的一个特殊情况。
今天给大家介绍的数学家就是亚历山大数学家——帕普斯.
帕普斯,Pappus,出生于公元330年,比中国的数学家刘徽(公元225-295)晚几十年。他出生的时候,距离罗马人占领亚历山大城过去了快500年。
在公元前2世纪,这个世界的东方西方开始都有了很大的改变。希腊西边的罗马终于打了过来,罗马武力强悍,最终铸就了雄伟的罗马帝国。而在东方,一个叫秦始皇的人武力爆表统一六国,秦朝二世而亡,汉朝建立,到汉武帝“罢黜百家独尊儒术”也不过百年,东方结束了从春秋战国开始的思想和文化最为璀璨灿烂的时代,西方也慢慢结束了古希腊的自由开放的学术探索思想。
帕普斯出生的年代相当于中国的东晋时期,那时距离古希腊黄金时代已经过去了几百年,理论几何逐渐衰落,在他之前也只有梅涅劳斯科普数学家·门纳劳斯·梅涅劳斯定理和托勒密科普数学家·托勒密·托勒密定理,而代数学只有丢番图一枝独秀。再过个100多年(也就是中国的南北朝时期),北方的野蛮人日耳曼会攻破西罗马,从此西方大陆从古典时代进入长达千年的黑暗时代,我们称呼它为为“黑暗的中世纪”。
至于中国没有黑暗的中世纪,为什么近代科学还是诞生在西方呢?个人觉得是“独尊儒术”的原因,导致中国并没有建立一个科学理论体系,陷入唯心主义的陷阱。当然肯定还有其他原因,我不是这个方面的专家,就不班门弄斧了。
现在回到帕普斯,他的主要成就是总结数百年的学者成果,以免年久失传。我们上一篇就写了,帕普斯称呼梅涅劳斯为亚历山大的梅涅劳斯,给历史留下了梅涅劳斯曾经存在的证据。
帕普斯给欧几里德和托勒密的著作都写过注解,他引用和参考了三十多位古代数学家的著作编写了《数学汇编》,这本书传播了大量的原始命题,进展,以及各种历史注解,给我们留下了解那些已经散失著作的机会,是一个名副其实的几何宝库。
帕普斯在数学历史中到现在还在用地以他名字命名的定理和方法。
第一个定理,称为帕普斯定理,交点共线问题。
就是开篇提到的“九树九行”那个有趣题目有关,定理是这样的:
- 平面六条直线u,v,w,x,y,z,如果:
- U与v的交点,x与w的交点,y与z的交点共线,
- 并且u与z的交点,x与v的交点,y与w的交点共线,
- 那么u与w的交点,x与z的交点,y与v的交点共线。
这个定理叫作帕普斯定理。
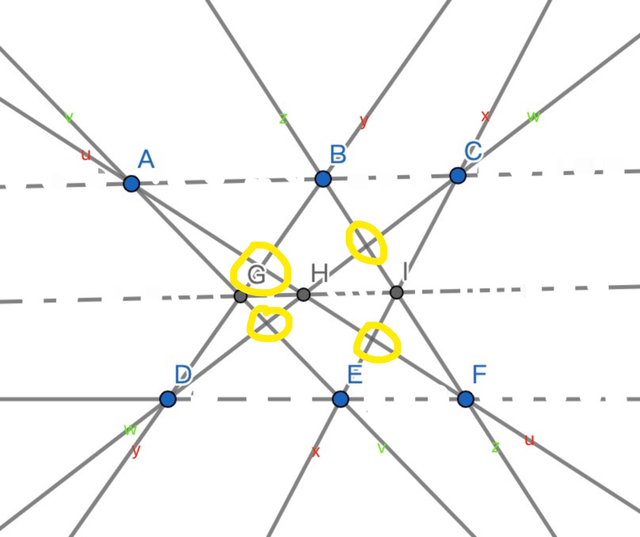
方便大家记忆和理解,
我画了一个图,六条直线分为两组,
红色组u,y,x,
绿色组v,z,w,
红色组和绿色组的交点是9个:A,B,C,D,E,F,G,H,I
(我们可以用组合计算下,共9个交点)
那么可以得到:
如果三点ABC共线,三点DEF共线,
那么剩余三点GHI也共线。
图上我用黄色标注出来的都是红色直线组内交点,或者绿色直线组内交点,还有2个没有画出来,比如绿色组的直线v和直线z交点,图上就没有。
这个定理可以证明3点共线,和梅涅劳斯定理一样。
还有我们开篇那道题,九树十行那道题是这个例子的特例,点BHE在一条直线上。如下图。
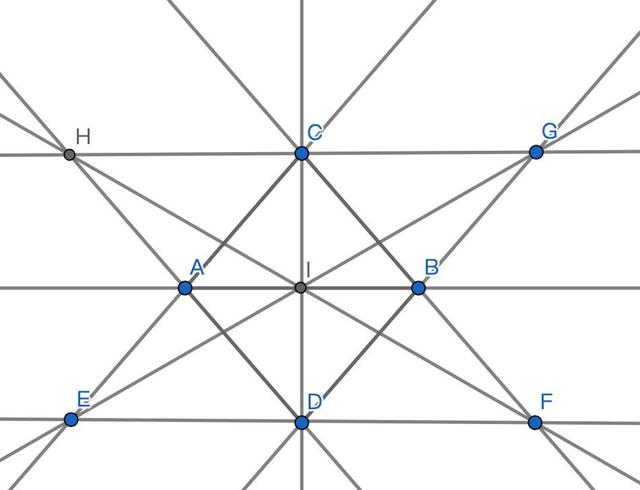
第二个帕普斯借助函数给出一种“三等分锐角”的方法。
众所周知的是用尺规是没办法三等分角的。帕普斯借助一个函数解决了三等分锐角的问题。
帕普斯是公元3世纪的人,直角坐标系是笛卡尔发明的,笛卡尔是17世纪人,那帕普斯那个时代怎么发明用直角坐标系函数解决问题的呢?但是我觉得这个解决方法很巧妙,也写出来吧。
步骤如下:
- 将锐角AOB置于平面直角坐标系中,o为原点,边ob放置在x轴上,a点在第一象限。
- 绘制函数y=1/x,和锐角aob相交于点d。
- 以d为圆心,2倍的od(de)长度为半径画圆,交y=1/x两个点,在角aob内的点f。
- 过d点做x轴平行线,过f点做y轴平行线,相交于g点。
- 那么角gob就是角aob的三等分角。
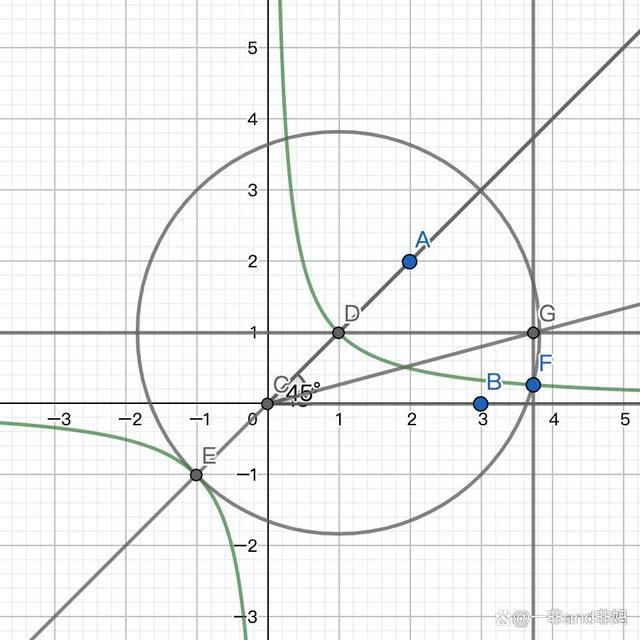
我用GGB做图,特意测量下了,角aob是45度,角gob等于15度,确实三等分了。
第三个中线定理,也称为(帕普斯定理),又称重心定理。
定理的内容是:三角形的一条中线两侧所对边平方的和等于底边的平方的一般加上这条中线长的平方的二倍。如下图就是:
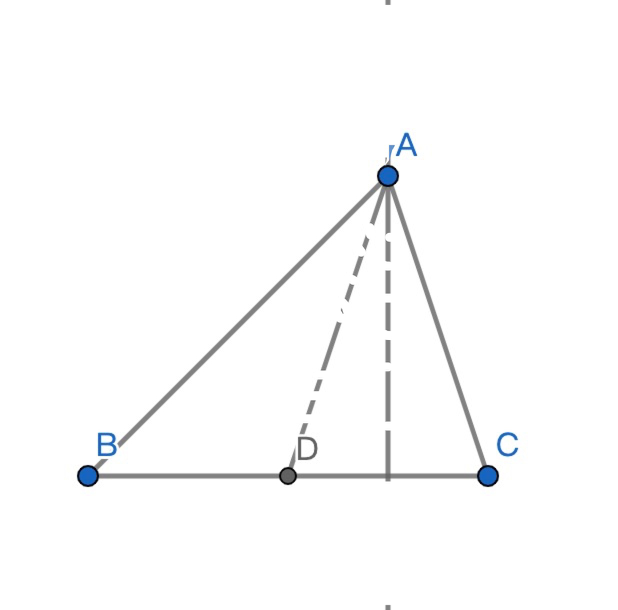
证明的话从A做BC的垂线,具体步骤就不写了。
第四个帕普斯表面积计算法则,也叫帕普斯-古尔丁第一定理。
为了计算旋转体的体积和表面积,帕普斯给出了一个法则,但是没有给出证明,瑞士数学家古尔丁1640年发表了证明,但是推理模糊不清,直到意大利数学家卡瓦利里用现代思想首先证明了。
这个定理方法帮助我们计算旋转体的表面积和体积,也可以帮助我们求弧线或面积的重心,中学物理竞赛中经常使用。
- 帕普斯表面积计算法则也称为帕普斯-古尔丁第一定理。
设一平面曲线位于直线的一侧,那么以直线为轴将曲线旋转一周360度,所产生的面积等于曲线的长度和曲线重心在旋转中所画的圆周长之积。
设曲线长为l,g是平面的重心到直线轴的距离,S为旋转面积:
S=2gl
2.帕普斯体积计算法则,也称为帕普斯-古尔丁第二定理。
设一平面区域在直线一侧,以直线为轴绕轴旋转一周360度,所产生的体积,等于平面区域的面积乘以面积重心在旋转中所画的圆周长。
设平面面积为S,平面重心到直线轴的距离为g,旋转体积为V,则:
V=2gS