1776年 清乾隆四十一年，纪晓岚、陆锡熊、戴震编纂武英殿聚珍版《孙子算经》，后世“鸡兔同笼”题的始祖

1776年 清乾隆四十一年，纪晓岚、陆锡熊、戴震编纂武英殿聚珍版《孙子算经》，后世“鸡兔同笼”题的始祖

数学珍贵古籍，清乾隆武英殿聚珍版【孙子算经】原装原签一厚册全，原装没有修补，精美白纸，推背图作者李淳风注释，《孙子算经》是中国古代重要的数学著作。约成书于四、五世纪，影响东南亚诸国深远，后世“鸡兔同笼”题的始祖。

《孙子算经》是中国古代重要的数学著作，成书大约在四、五世纪，也就是大约一千五百年前，作者生平和编写年不详。传本的《孙子算经》共三卷。卷上叙述算筹记数的纵横相间制度和筹算乘除法，卷中举例说明筹算分数算法和筹算开平方法。卷下第31题，可谓是后世“鸡兔同笼”题的始祖，后来传到日本，变成“鹤龟算”。书中是这样叙述的：“今有雉兔同笼，上有三十五头，下有九十四足，问雉兔各几何？这四句话的意思是：有若干只鸡兔同在一个笼子里，从上面数，有35个头；从下面数，有94只脚。求笼中各有几只鸡和兔？

具有重大意义的是卷下第26题：“今有物不知其数，三三数之剩二，五五数之剩三，七七数之剩二，问物几何？答曰：‘二十三’”。《孙子算经》不但提供了答案，而且还给出了解法。南宋大数学家秦九韶则进一步开创了对一次同余式理论的研究工作，推广“物不知数”的问题。德国数学家高斯[K.F. Gauss.公元1777-1855年]于公元1801年出版的《算术探究》中明确地写出了上述定理。公元1852年，英国基督教士伟烈亚士[Alexander Wylie公元1815-1887年]将《孙子算经》“物不知数”问题的解法传到欧洲，公元1874年马蒂生[L.Mathiesen]指出孙子的解法符合高斯的定理，从而在西方的数学史里将这一个定理称为“中国的剩余定理”[Chinese remainder theorem]。另外还有一道，曰：“巍巍古寺在山林，不知寺内几多僧。三百六十四只碗，看看用尽不差争。三人共食一碗饭，四人共吃一碗羹。请问先生明算者，算来寺内几多僧。”

上卷

详细的讨论了度量衡的单位和筹算的制度和方法。

度量衡包括长度（度），质量（量），体积/容积（衡）。长度的基本单位是蚕吐出的一根丝（直径为一忽），以上为十进。小的长度单位包括忽，丝，毫，牦，分，寸，尺，丈，引，端（50引）。辅助单位包括匹（40尺），步（6尺），亩（240步。古代以方形周长代面积），里（300步）。

质量的基本单位是一颗黍的质量，以上是絫，铢，两（24铢），觔（即斤，16两），钧（30斤），石（4钧）。

体积和容积的基本单位是一颗粟的体积。以上是圭（6粟），撮，抄，勺，合，升，斗，斛。
大数的名称，一万万为亿，以上每一万倍称为兆，京，陔，秭，穣，沟，涧，正，载。
圆周率约等于三（周三径一），根号2约等于1.4（方五斜七）。

以下还记载了白银，铅，铜，铁，玉，石等生产生活和经济生活中常见的物质的密度。

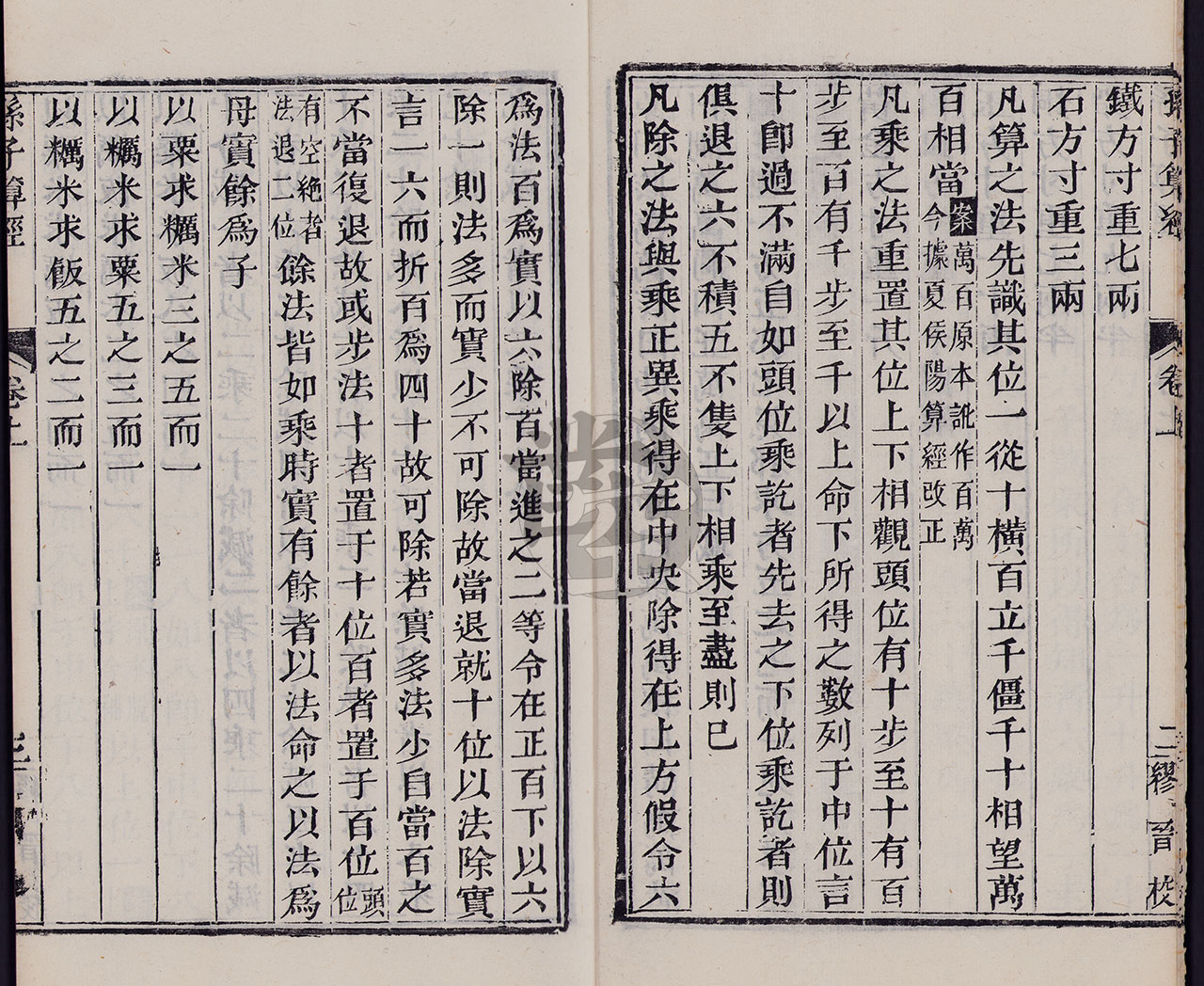
筹算在春秋战国时代已经运用，但在古代中国数学著作如算数书、九章算术等书中都不曾记载算筹的使用方法；孙子算经第一次详细地记述筹算的布算规则：“凡算之法，先识其位，一纵十横，百立千僵，千十相望，百万相当”，此外又说明用空位表示零。

在进行乘法时，“凡乘之法，重置其位。上下相观，上位有十步至十，有百步至百，有千步至千。以上命下，所得之数列于中位。言十即过，不满自如。上位乘讫者先去之。下位乘讫者则俱退之。六不积，五不只。土下相乘，至尽则已。”《孙子算经》明确说明“先识其位”的位值概念，和“逢十进一”的十进位制。

除法法则：“凡除之法：与乘正异乘得在中央，除得在上方，假令六为法，百为实，以六除百，当进之二等，令在正百下。以六除一，则法多而实少，不可除，故当退就十位，以法除实，言一六而折百为四十，故可除。若实多法少，自当百之，不当复退，故或步法十者，置于十百位（头位有空绝者，法退二位。余法皆如乘时，实有余者，以法命之，以法为母， 实余为子。”）

在此之后记载了谷物换算成精谷物和米饭的经验比例：粟米打成粝米的体积是五分之三，粝米煮成米饭的体积是二分之五。

第一章的最后是乘法表（从九九八十一开始到一一得一）和每个乘法结果的乘方表。用表格记载下来如下：

《孙子算经》乘法表：

中卷：

主要是关于分数的应用题，包括面积、体积、等比数列等计算题，大致都在《九章》中论述的范围之内；

下卷：

对后世的影响最为深远，如下卷第31题即著名的“鸡兔同笼”问题，后传至日本，被改为“鹤龟算”。今有雉、兔同笼，上有三十五头，下有九十四足。问：雉、兔各几何？答曰：雉二十 三，兔一十二。术曰：上置三十五头，下置九十四足。半其足，得四十七，以少减多，再命之，上三 除下三，上五除下五，下有一除上一，下有二除上二，即得。又术曰：上置头，下置足，半其足，以头除足，以足除头，即得。

算法译文：第一行放好头的数目，第二行放好脚的数目。将脚的数目除以二，得四十七。以较少的头数减较多的”脚数的一半“，得十二（现在我们知道这就是兔的数目），将第一行的算筹数目根据第二行得出的数目依次取去，即得鸡的数目。

另一种算法是：第一行放头的数目，第二行放脚的数目，将脚的数目除以二，从脚的数目的一半减去头的数目，再从头的数目减去刚才所获得的结果，即得鸡的数目。

下卷27题则是”鸡兔同笼“的一种推广。即使是头多于一个的奇异生物也能计算它们的数量。
今有兽，六首四足；禽，四首二足，上有七十六首，下有四十六足。问：禽、兽各几何？答曰：八兽、七禽。术曰：倍足以减首，余半之，即兽；以四乘兽，减足，余半之，即禽。

算法译文：将脚的总数乘以二，减去头的数目，差除以二，得到兽的数目。将兽的数目乘以四，减去脚的数目，除以二，得到禽的数目。

下卷第28题“物不知数”为后来的“大衍求一术”的起源，被看作是中国数学史上最有创造性地成就之一，称为中国余数定理：今有物，不知其数。三三数之，剩二；五五数之，剩三；七七数之，剩二。问：物几 何？答曰：二十三。

术曰：三三数之，剩二，置一百四十；五五数之，剩三，置六十三；七七数之，剩二 ，置三十。并之，得二百三十三，以二百一十减之，即得。凡三三数之，剩一，则置七十 ；五五数之，剩一，则置二十一；七七数之，剩一，则置十五。一百六以上，以一百五 减之，即得。

下卷最后一题还提供了一种卜算胎儿性别的”方法“，颇有些现代”校验算法“的旨趣，一并记之如下：
今有孕妇，行年二十九岁。难九月，未知所生？答曰：生男。

术曰：置四十九加难月，减行年，所余以天除一，地除二，人除三，四时除四，五行除五，六律除六，七星除七，八风除八，九州除九。其不尽者，奇则为男，耦则为女。

算法译文：基数七七四十九，加上孕妇的孕期（九月，得五十八），减去孕妇的年龄（二十九，得二十九）。计算结果连续除以一到九的整数。如果最后余数的和是奇数就是生男，偶数就是生女。本例的结果是0、1、2、1、4、5、1、5、2，和为21，所以孕妇生的是男孩。

剩余定理：

在我国古代劳动人民中，长期流传着“隔墙算”、“剪管术”、“秦王暗点兵”等数学游戏。有一首“孙子歌”，甚至远渡重洋，输入日本：

“三人同行七十稀，五树梅花廿一枝，
七子团圆正半月，除百零五便得知。”

这些饶有趣味的数学游戏，以各种不同形式，介绍世界闻名的“孙子问题”的解法，通俗地反映了中国古代数学一项卓越的成就。“孙子问题”在现代数论中是一个一次同余问题，它最早出现在我国公元四世纪的数学著作《孙子算经》中。《孙子算经》卷下“物不知数”题说：有物不知其数，三个一数余二，五个一数余三，七个一数又余二，问该物总数几何？显然，这相当于求不定方程组  N=3x+2,N=5y+3,N=7z+2  的正整数解N，或用现代数论符号表示，等价干解下列的一次同余组。
N=2(mod3);N=3(mod5);N=2(mod7) 《孙子算经》所给答案是N=23。由于孙子问题数据比较简单，这个答数通过试算也可以得到。但是《孙子算经》并不是这样做的。“物不知数”题的术文指出解题的方法多三三数之，取数七十，与余数二相乘；五五数之，取数二十一，与余数三相乘；七七数之，取数十五，与余数二相乘。将诸乘积相加，然后减去一百零五的倍数。列成算式就是：N=70×2+21×3+15×2－2×105=23。

这里105是模数3、5、7的最小公倍数，容易看出，《孙子算经》给出的是符合条件的最小正整数。对于一般余数的情形，《孙子算经》术文指出，只要把上述算法中的余数2、3、2分别换成新的余数就行了。以R1、R2、R3表示这些余数，那么《孙子算经》相当于给出公式
N=70×R1+21×R2+15×R3－P×105（p是整数）。

孙子算法的关键，在于70、21和15这三个数的确定。后来流传的《孙子歌》中所说“七十稀”、“廿一技”和“正半月”，就是暗指这三个关键的数字。《孙子算经》没有说明这三个数的来历。实际上，它们具有如下特性：

也就是说，这三个数可以从最小公倍数M=3×5×7=105中各约去模数3、5、7后，再分别乘以整数2、1、1而得到。假令k1=2，K2=1，K3=1，那么整数Ki（i=1，2，3）的选取使所得到的三数70、21、15被相应模数相除的时候余数都是1。由此出发，立即可以推出，在余数是R1、R2、R3的情况下的情况。

应用上述推理，可以完全类似地把孙子算法推广到一般情形：设有一数N，分别被两两互素的几个数a1、a2、……an相除得余数R1、R2、……Rn，即
N≡Ri（mod ai）（i=1、2、……n），
只需求出一组数K，使满足
1（mod ai）（i=1、2、……n），
那么适合已给一次同余组的最小正数解是
（P是整数，M=a1×a2×……×an），

这就是现代数论中著名的剩余定理。如上所说，它的基本形式已经包含在《孙子算经》“物不知数”题的解法之中。不过《孙子算经》没有明确地表述这个一般的定理。

孙子问题出现在公元四世纪的中国算书中，这并不是偶然的。我国古代天文历法资料表明，一次同余问题的研究，明显地受到天文、历法需要的推动，特别是和古代历法中所谓“上元积年”的计算密切相关。大家知道，一部历法，需要规定一个起算时间，我国古代历算家把这个起点叫做“历元”或“上元”，并且把从历元到编历年所累积的时间叫做“上元积年”。上元积年的推算需要求解一组一次同余式。以公元三世纪三国时期魏国施行的《景初历》做例，这部历法规定以冬至、朔旦（朔日子夜）和甲子日零时会合的时刻作为历元。设a是一回归年日数，b是一朔望月日数，当年冬至距甲子日零时是R1日，离平朔时刻是R2日，那么《景初历》上元积元数N就是同余组的解。aN≡Ri（mod 60）≡R2（mod b）

到了南北朝时期，祖冲之《大明历》（公元462年）更要求历元必须同时是甲子年的开始，而且“日月合璧”、“五星联珠”（就是日、月、五大行星处在同一方位），月亮又恰好行经它的近地点和升交点。这样的条件下推算上元积年，就相当于要求解十个同余式了。天文历法数据一般又都十分庞杂，所以，在《孙子算经》成书前后的魏晋南北朝时期，我国的天文历算家无疑已经能够求解形式比《孙子算经》“物不知数”题复杂得多的一次同余式，因而必定掌握了按一定程序计算一次同余式的方法。《孙子算经》比例题的形式总结、反映了这一事实。以后天文历算家长期沿用孙子算法推算上元积年，这中间肯定会引起更加深入的探讨。到公元十三世纪，大数学家秦九韶集前法之大成，终于在一次同余式的研究上获得了超越前人的辉煌成果。

秦九韶，字道古，生活于南宋时期，自幼喜好数学，经过长期积累和苦心钻研，干公元1247年写成《数书九章》。这部中世纪的数学杰作，在许多方面都有创造，其中求解一次同余组的“大衍求一术”和求高次方程数值解的“正负开方术”，更是具有世界意义的成就。

这里主要介绍秦九韶对一次同余论的伟大贡献。

秦九韶在《数书九章》中明确地系统地叙述了求解一次同余组

的一般计算步骤。秦的方法，正是前述的剩余定理。我们知道，剩余定理把一般的一次同余问题归结为满足条件的一组数Ki，的选定。秦九韶给这些数起名叫“乘率”，并且在《数书九章》卷一“大衍总术”中详载了计算乘率的方法——“大衍求一术”。

为了介绍“大衍求一术”，我们以任一乘率ki的计算作例。如果Gi=>ai，秦九韶首先令ai除Gi，求得余数gi
Gi≡gi（mod ai），
于是 kiGi≡Kigi（mod ai），
但是因为 kiGi≡1（mod ai），

所以问题归结为求ki使适合kigi≡1（mod ai）。秦九韶把ai叫“定数”，gi叫“奇数”，他的“大衍求一术”，用现代语言解释，实际就是把奇数gi和定数ai辗转相除，相继得商数q1、q2、……qn和余数r1、r2、……rn，在辗转相除的时候，随即算出下面右列的c值：

秦九韶指出，当rn=1而n是偶数的时候，最后得到的cn就是所求乘率ki。如果rn=1而n是奇数，那么把rn－1和rn相除，形式上令qn+1=rn-1－1，那么余数rn+1仍旧是1，再作cn+1=qn+1cn+cn-1,qn+1=rn-1-1是偶数，cn+1就是所求的ki。不论哪种情形，最后一步都出现余数1，整个计算到此终止，秦九韶因此把他的方法叫做“求一术”（至于“大衍”的意思，秦九韶本人在《数书九章》序中把它和《周易》“大衍之数”相附会）。可以证明，秦九韶这一算法是完全正确，十分严密的。

在秦九韶那个时代，计算仍然使用算筹。秦九韶在一个小方盘上，右上布置奇数g，右下布置定数a，左上置1（他叫它做“天元1”），然后在右行上下交互以少除多，所得商数和左上（或下）相乘并入左下（或上），直到右上方出现1为止。下页就是秦九韶的一般筹算图式，右边是一个数字例子（g=20，a=27，K=C4=23）。

秦九韶在《数书九章》中采集了大量例题，如“古历会积”、“积尺寻源”、“推计土功”、“程行计地”等等，广泛应用大衍求一术来解决历法、工程、赋役和军旅等实际问题。在这些实际问题中，模数ai并不总是两两互素的整数。秦九韶区分了“元数”（ai是整数）、“收数”（ai是小数）、“通数”（ai是分数）等不同情形，并且对每种情形给出了处理方法。“大衍总术”把“收数”和“通数”化成“元数”的情形来计算，而对于元数不两两互素的情形，给出了可靠的程序，适当选取那些元数的因子作定数而把问题归结为两两互素的情形。所有这些系统的理论，周密的考虑，即使以今天的眼光看来也很不简单，充分显示了秦九韶高超的数学水平和计算技巧。秦九韶小时曾跟随他父亲到南宋京城杭州，向太史局（主管天文历法的机构）的官员学习天文历法，“大衍求一术”很可能就是他总结天文历法计算上元积年方法的结果。但是“大衍求一术”似乎没有为他同时代的人所充分理解。明中叶以后几乎失传。一直到清代，“大衍求一术”又重新被发掘出来，引起了许多学者（张敦仁、李锐、骆腾凤、黄宗宪等）的兴趣。他们对“大衍求一术”进行了解释、改进和简化，其中黄宗宪《求一术通解》对模数非两两互素的情形给出了更加简明的方法，但是时代已是晚清。

从《孙子算经》“物不知数”题到秦九韶的“大衍求一术”，古代中国数学家对一次同余式的研究，不仅在中国数学史上而且在世界数学史上占有光荣的地位。在欧洲，最早接触一次同余式的，是和秦九韶同时代的意大利数学家裴波那契（1170—1250），他在《算法之书》中给出了两个一次同余问题，但是没有一般的算法。这两个问题从形式到数据都和孙子物不知数题相仿，整个水平没有超过《孙子算经》。直到十八、十九世纪，大数学家欧拉（1707—1783）于公元1743年、高斯（1777—1855）于公元1801年对一般一次同余式进行了详细研究，才重新获得和秦九韶“大衍求一术”相同的定理，并且对模数两两互素的情形给出了严格证明。欧拉和高斯事先并不知道中国人的工作。公元1852年英国传教士伟烈亚力（1815—1887）发表《中国科学摘记》，介绍了《孙子算经》物不知数题和秦九韶的解法，引起了欧洲学者的重视。1876年，德国马蒂生（1830—1906）首先指出孙子问题的解法和高斯方法一致，当时德国著名数学史家康托（1829—1920）看到马蒂生的文章以后，高度评价了“大衍术”，并且称赞发现这一方法的中国数学家是“最幸运的天才”。直到今天，“大衍求一术”仍然引起西方数学史家浓厚的研究兴趣。如1973年，美国出版的一部数学史专著《十三世纪的中国数学》中，系统介绍了中国学者在一次同余论方面的成就，作者力勃雷希（比利时人）在评论秦九韶的贡献的时候说道：“秦九韶在不定分析方面的著作时代颇早，考虑到这一点，我们就会看到，萨顿称秦九韶为‘他那个民族、他那个时代、并且确实也是所有时代最伟大的数学家之一’，是毫不夸张的。”

印度学者对一次同余论也有过重要贡献。从公元六世纪到十二世纪，他们发展了一种称为“库塔卡”的算法，用来求解和一次同余式等价的不定方程组。“库塔卡”法出现在孙子算法之后，印度数学家婆罗门复多（七世纪）、摩柯吠罗（九世纪）等人的著作中，都有和物不知数题相同的一次同余问题。这当然不是要借此断言“库塔卡”法一定受到了孙子算法的影响，但是有人（如万海依等）硬说中自的“大衍求一术”来源于“库塔卡”，就是毫无根据的妄说了。万海依居然把中国算法中数码从左到右横写作为“大衍术”受印度影响的重要根据。大家知道，中国古代至迟从春秋战国时期就开始使用算筹记数，我们今天还可以从现存的公元前三世纪的货币上看到这种从左到右的记数方法。由此可见，万海依的论点多么荒唐可笑。中国古代数学家对一次同余论的研究有明显的独创性和继承性，“大衍求一术”在世界数学史上的崇高地位是毋容置疑的，正因为这样，在西方数学史著作中，一直公正地称求解一次同余组的剩余定理为“中国剩余定理”。

荡杯问题

在中国古算书中，《孙子算经》一直在我国数史占有重要的地位，其中的“盈不足术”、“荡杯问题”等都有着许多有趣而又不乏技巧算术程式。

孙子算经.卷下第十七问给我们描述的就是著名的“荡杯问题”的程式。题曰：“今有妇人河上荡杯。津吏问曰：‘杯何以多？’妇人曰：‘有客。’津吏曰：‘客几何？’妇人曰：‘二人共饭，三人共羹，四人共肉，凡用杯六十五。不知客几何？”

很明显，这里告诉我们这次洗碗事件，要处理的是65个碗共有多少人的问题。其中有能了解客数的信息是2人共碗饭，3人共碗羹，4人共碗肉。通过这几个数值，很自然就能解决客数问题。因为客数是固定值，因此将其列成今式为N/2+N/3+N/4=65，易得客数六十人。

而该题的解法与今解如出一辙，其有“术曰：置六十五杯，以一十二乘之，得七百八十，以十三除之，即得”可证。