1877年 光绪三年 江南机器制造局精印《测海山房》3、4册,增珠算大成典籍 算法统宗11卷全
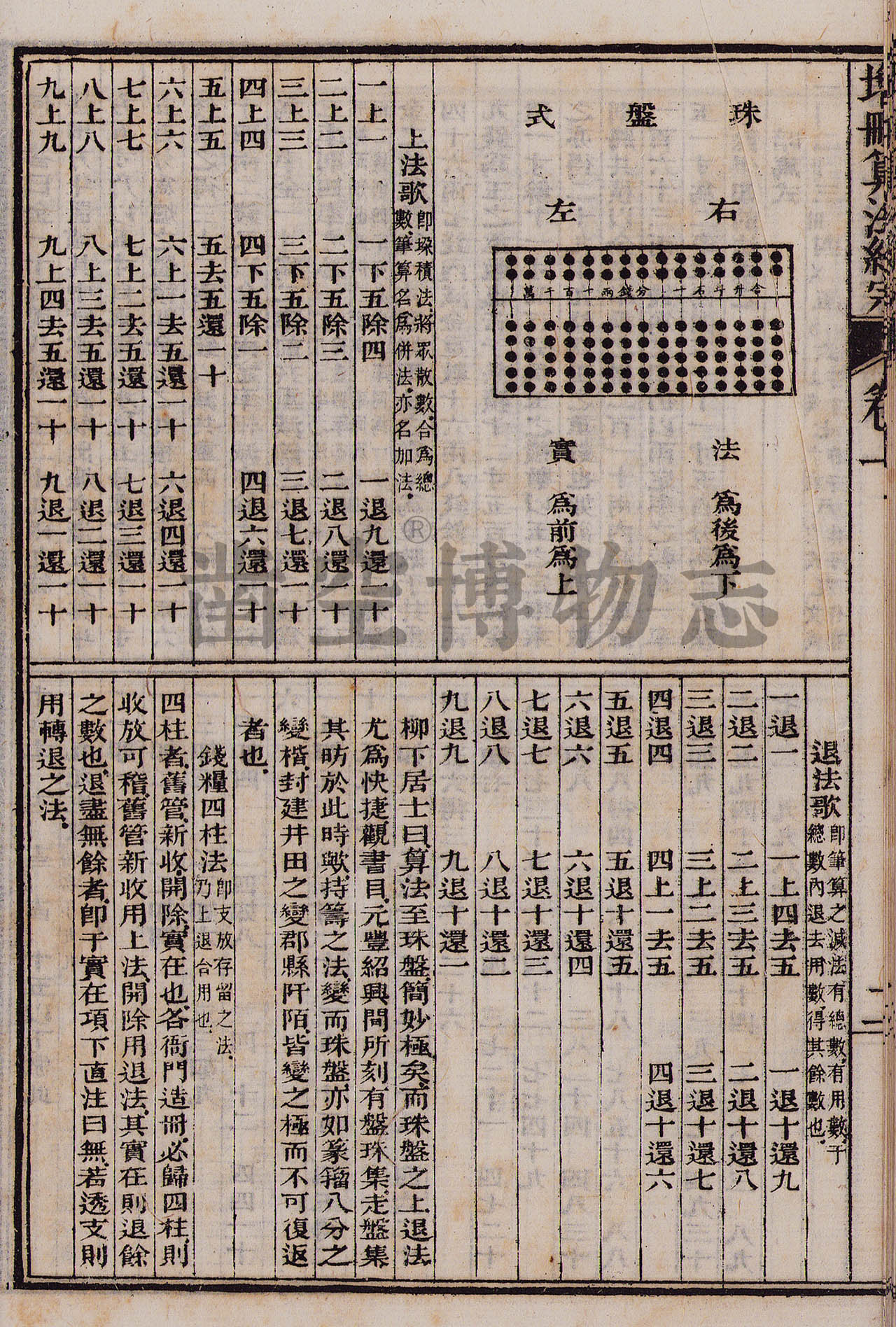
《算法统宗》全称《新编直指算法统宗》,是中国古代数学名著,程大位著。《算法统宗》17卷,卷1、卷2介绍数学名词、大数、小数和度量衡单位以及珠算盘式图、珠算各种算法口诀等,并举例说明具体用法;卷3至卷12按“九章”次序列举各种应用题及解法;卷13到卷16为“难题”解法汇编;卷17“杂法”,为不能归入前面各类的算法,并列有14个纵横图。书后附录“算经源流”一篇,著录了北宋元丰七年(1084年)以来的数字书目51种。万历二十一年(1593年)刊行。
《算法统宗》是一部应用数学书,是以珠算为主要的计算工具,列有595个应用题的数字计算,都不用筹算方法,而是用珠算演算。评述了珠算规则,完善了珠算口诀,确立了算盘用法,完成了由筹算到珠算的彻底转变。《算法统宗》绝大多数的问题都是从其他数学著作如刘仕隆所著《九章通明算法》(公元1424元)和吴敬的《九章算法比类大全》(公元1450年)等书中摘取出来的。
《算法统宗》从初版至民国时期,出现了很多不同的翻刻本、改编本,民间还有各种抄本流传,对我国民间普及珠算和数学知识起到了很大的作用。明末,日本人毛利重能将《算法统宗》译成日文,开日本“和算”先河。清初,该书又传入朝鲜、东南亚和欧洲,成为东方古代数学的名著。
在中国古代数学的整个发展过程中来看,《算法统宗》是一部十分重要的著作。从流传的长久,广泛和深入程度来讲,是任何一部数学著作不能与其相比的。
程大位(1533-1606)字汝思,号宾渠,南直隶徽州府休寧县率口(今安徽屯溪市)人。明代商人、珠算家。一生未仕,20岁起便在长江中下游一带经商,因商业计算需要,遍访名师,搜集数学书籍,参考各家学说,加以己意,于60岁时完成《直指算法统宗》(简称《算法统宗》)。英国李约瑟说:“明代数学家中,最引人注目的是程大位”,“在程大位《直指算法统宗》以前,没有任何关于近代珠算的完整叙述”。
明代在西方数学输入之前,最大的成就可以说是珠算的发明,最重要的数学书要算程大位的《算法统宗》(1592)。在电子计算机普及之前,算盘以其构造简单,价格低廉,计算迅速,数百年来受到广大群众的欢迎,至今仍盛行不衰,“珠算”的名称,在《数术记遗》中已经出现,这可能是后世珠算的萌芽,可惜该书描述过简,未知其详。
我国历来注重计算器械,从算筹发展到算盘是很自然的事明朝陶宗仪《辍耕录》(1366)有“算盘珠”的比喻:“算盘珠,言拨之则动”。明朝吴敬(杭州府仁和县人)1450年撰《九章算法比类大全》有“不用算盘,至无差误”;“免用算盘并算子,乘除加减不为难”等话,这是提到算盘的最早数学著作。
确实可考的记述算盘的书,以柯尚迁《数学通轨》(1578)为最早,其中载有十三桁的算盘,和现在的形式完全一样,并有计算歌诀,到程大位的《算法统宗》,详述算盘的制度和用法,珠算到此已完全成熟。
程大位字汝思,号宾渠,新安人,生于1533年,在1592年编成《直指算法统宗》(简称《算法统宗》,万历二十一年(1593)渐江(即浙江)吴继绶作序,这是流传很广的一部书,卷二列有算盘的式样,和各种运算口诀,是后世珠算口诀的样本,
《算法统宗》内容丰富,但除了算盘和歌诀之外,没有新的创造,基本上是整理前人作品的书。并且还漏掉了高次方程和多元高次方程等重要部分。
相传明末日本毛利重能到中国学数学,把《算法统宗》带回去。他所著的《割算书》(1622)和他的门徒吉田光由(1598—1672)所著《尘劫记》(1627)都记述珠算方法,不过算盘或者在《算法统宗》之前就已流入了日本。
日本算盘叫“十露盘”,算珠由圆形改成菱形(纵截面),梁上两珠变成一珠,现在我国东北所使用的算盘就是这一种,比关内算盘小得多,狭而长(常见的有7×38cm)桁数多至27。
希腊时代也有“算盘”不过和现在的算盘是两回事。在一个盘上刻划许多直行或横行,用石子或木钉放在行上记数,这是最原始的记数方法,同时,画几何图或记数的沙板也叫算盘,后来转成拉丁文abacus或abax及英文abacus。
罗马改良了这种算盘。在盘上刻槽,槽内放置珠子,也可以拿走,再进一步将珠子嵌在金属制的槽里面,可以上下移动,不可以拿走,罗马人不懂位值制记数法,算盘的槽上要刻字母表示单位,另一方面,他们又用12进分数,在算盘上另添小槽表示分数,通分加减,十分麻烦。
西方人没有九九乘法口诀,我国文字一字一音,编成口诀,顺口流利,外文一字数音,不便口诀化。
罗马算盘是铜制的,价昂贵不利于普及,而且很笨重,不象中国算盘的竹制的,轻便而价廉,罗马算盘的这些缺点,使得它逐渐被淘汰,最后成为博物馆的陈列品,欧洲人又回到摆石子的“算板”(counting board )的老路上去。
古俄罗斯人也有一种算盘,若干弧形的木条,横着镶在木框内,每条穿着十个珠子,珠子一当一,二当二,不象中国上珠一当五,下珠一当一,因此计算速度大受限制。